Riddles are like tiny mental workouts. They challenge our logic, stretch our creativity, and often leave us either triumphant or scratching our heads. Here’s one riddle that has stumped many and sparked endless debates:
What comes once in a year, twice in a month, four times in a week, and six times in a day?
Sounds simple, right? But as you dig deeper, the answer becomes elusive. Before we reveal the solution, take a moment to think. Got your guess? Let’s dive into the layers of this intriguing puzzle.
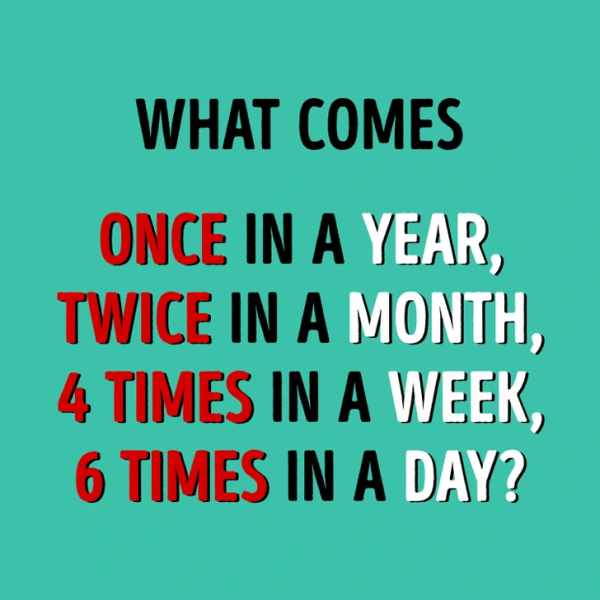
Why This Riddle Captures Attention
At first glance, this riddle seems like a straightforward question about time or events. However, its simplicity is deceptive. The phrasing plays with familiar units of time—year, month, week, and day—which naturally leads us to think in terms of calendars, dates, or schedules. But the key to solving it lies in stepping back and looking for patterns rather than literal interpretations.
Common Pitfalls When Solving This Riddle
Solving riddles requires a mix of logic, observation, and abstract thinking. Here are the traps people often fall into when tackling this one:
- Literal Thinking: Most assume the answer involves actual events, like holidays or weekends, but this leads down the wrong path.
- Overcomplication: Some try to factor in leap years, lunar months, or intricate calendar systems, which only clouds the simplicity of the riddle.
- Ignoring Numerical Hints: The progression (once, twice, four times, six times) is a vital clue that many overlook.
To crack this riddle, you need to focus on patterns and relationships between numbers, not tangible occurrences.
Step-by-Step Breakdown of the Riddle
Let’s analyze the riddle systematically and uncover its clever logic.
Step 1: Focus on the Clues
The riddle gives us four specific time frames:
- Once in a year
- Twice in a month
- Four times in a week
- Six times in a day
This sequence hints at a recurring pattern that becomes more frequent as the time unit shrinks.
Step 2: Eliminate Literal Interpretations
While it’s tempting to think of holidays or events, these don’t fit the numerical progression. For example:
- Holidays like Christmas happen once a year but not twice in a month.
- Weekends occur multiple times in a week but not in the specified progression.
Clearly, the riddle isn’t pointing to tangible events but rather an abstract concept.
Step 3: Look for Numerical Patterns
Here’s the breakthrough: the numbers (once, twice, four times, six times) correspond to odd occurrences. Let’s break it down:
- Once in a Year: The number “1” appears once in the sequence, indicating a singular odd occurrence.
- Twice in a Month: Over a typical month, there are two odd-numbered weeks.
- Four Times in a Week: Each week has four odd-numbered days (e.g., 1, 3, 5, 7).
- Six Times in a Day: In a 12-hour clock, there are six odd hours (1, 3, 5, 7, 9, 11).
The Answer Revealed: It’s All About “Odd”
The answer to the riddle lies in odd occurrences or odd numbers. The pattern aligns perfectly with the odd-numbered frequency across different time units:
- Once in a year: A single odd occurrence.
- Twice in a month: Two odd-numbered weeks.
- Four times in a week: Four odd days.
- Six times in a day: Six odd hours.
This solution is as elegant as it is logical, proving that sometimes the simplest explanations are the most satisfying.

Why This Riddle Is a Brain-Teaser
What makes this riddle so tricky? It’s the clever misdirection. By framing the question with familiar time units, the riddle nudges you to think about specific events or tangible objects. However, the actual solution lies in recognizing abstract numerical patterns. It’s a reminder to think outside the box and approach puzzles from multiple angles.
The Joy of Solving Riddles
Riddles like this one aren’t just fun; they’re excellent for sharpening your mind. They encourage you to:
- Analyze Patterns: Finding order in chaos is a critical problem-solving skill.
- Think Creatively: Abstract thinking helps you uncover solutions that aren’t immediately obvious.
- Be Patient: Riddles teach us the value of slowing down and considering all possibilities.
Whether you cracked the riddle on your own or learned the answer here, you’ve exercised your brain in a meaningful way.
What Was Your First Guess?
Now that you know the answer, how close were you? Did you immediately think of odd numbers, or were you led astray by literal interpretations? Share your thoughts in the comments—let’s see how many of you were on the right track!
Conclusion: Keep Challenging Yourself
Riddles like this one remind us that the simplest puzzles can offer the most profound lessons. They challenge our assumptions, push us to think critically, and reward us with a sense of accomplishment when we solve them.
So, the next time you encounter a riddle, embrace the challenge. Look for patterns, think outside the box, and don’t be afraid to make mistakes. After all, every puzzle you solve sharpens your mind and prepares you for the next one.
Ready for your next challenge? Keep exploring the world of riddles and puzzles—you never know what fascinating logic you’ll uncover next!